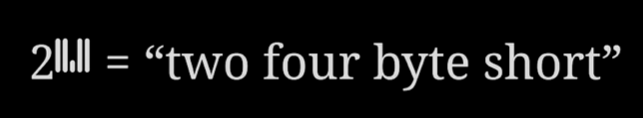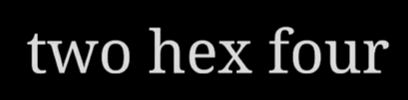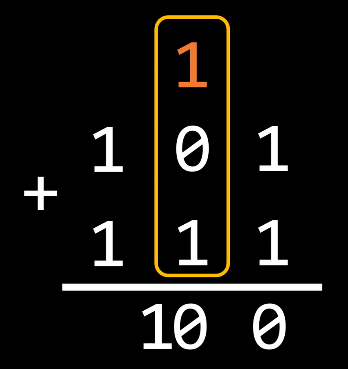web/content/notes/ready/binary-operations/index.md

title, description, date, draft, tags, author, showToc

title	description	date	draft	tags	author	showToc
Binary Operations		2025-02-17T08:37:24+00:00	false	computer-science	TrudeEH	true

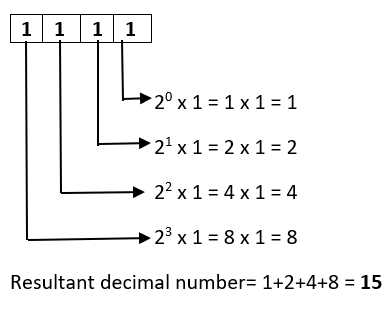
Binary

Binary is a base-2 numeral system: A simple way to represent numbers using only two states.

Binary	Decimal	Hexadecimal
0000	00	00
0001	01	01
0010	02	02
0011	03	03
0100	04	04
0101	05	05
0110	06	06
0111	07	07
1000	08	08
1001	09	09
1010	10	0A
1011	11	0B
1100	12	0C
1101	13	0D
1110	14	0E
1111	15	0F

Speaking Binary

The information in this section is non-standard, and mostly a curiosity.

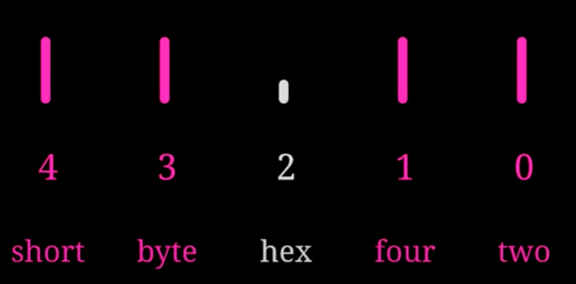
You may struggle to pronounce large binary numbers, as saying a long list of 0s and 1s is very inefficient. Instead, we can do something like this:

To be able to say any binary number, list the number, starting by the last digit:

And pronounce the ones that correspond to a 1 bit.

Pronounce a Binary Number at a Glance

1. Break the number at its largest pair of bits.

   

2. Represent the left and right sides.

   

   In this example, there is a two in the order of magnitude hex.

3. Continue to represent the left and right sides recursively.

   

   The last number is four.

Decode a Spoken Binary Number

Starting with two hex four:

1. Find the largest power of two.

   

2. The number is equal to the left side, times the order of magnitude, plus the right side.

   

Avoiding Repetition

Repetition can be avoided by combining some very common, small numbers:

These shortcuts essentially create a quaternary system to pronounce binary, but in this case, the result improves spoken efficiency by a lot.

Arithmetic Operations

Addition

Adding two numbers can be done using a simple, manual algorithm: By adding the last bit of both numbers first, carry if necessary, then move on to the next number, and so on.

+	0	1
0	0	1
1	1	10

To add numbers more efficiently by hand, you can group bits together and memorize the patters, effectively doubling your speed.

To improve calculation speed even further, you can group more bits, and learn those patterns as well.

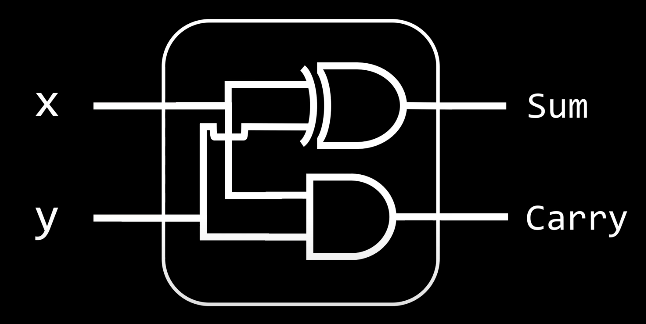
Half Adder

Add 2, single-digit binary numbers.

A	B	Carry	Sum
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

!

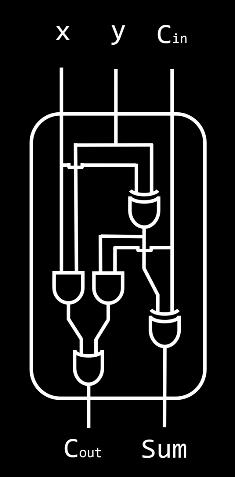
Full Adder

When adding 2 binary numbers, one operation might return a carry value, which the half adder can't accept, as it only has 2 inputs.

!

To solve this issue, a full adder accepts 3 inputs.

!

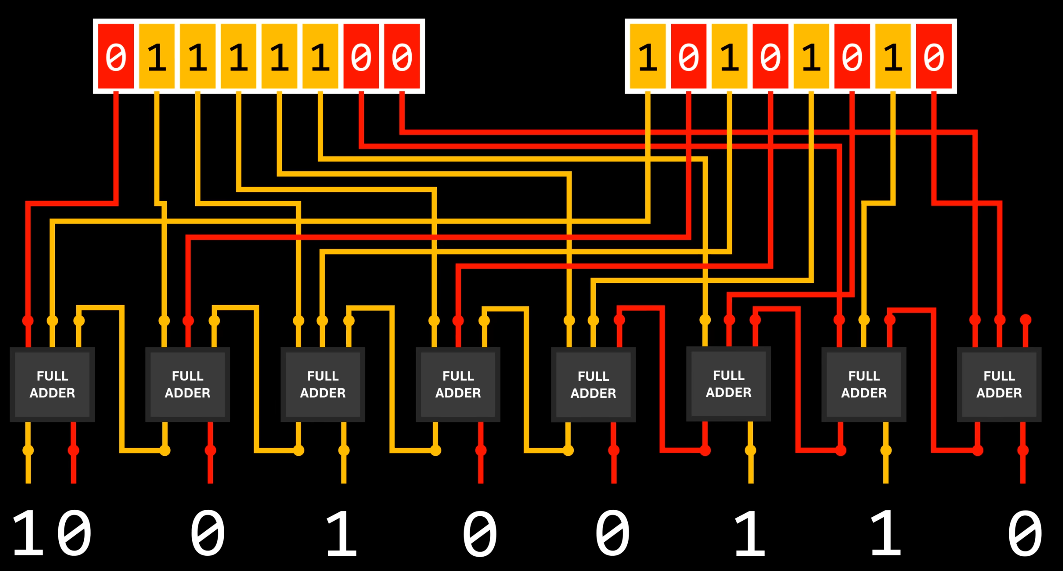
8-Bit Adder

!

Subtraction

Subtraction can result in negative numbers. Like how additions need a carry, subtraction needs a borrow.

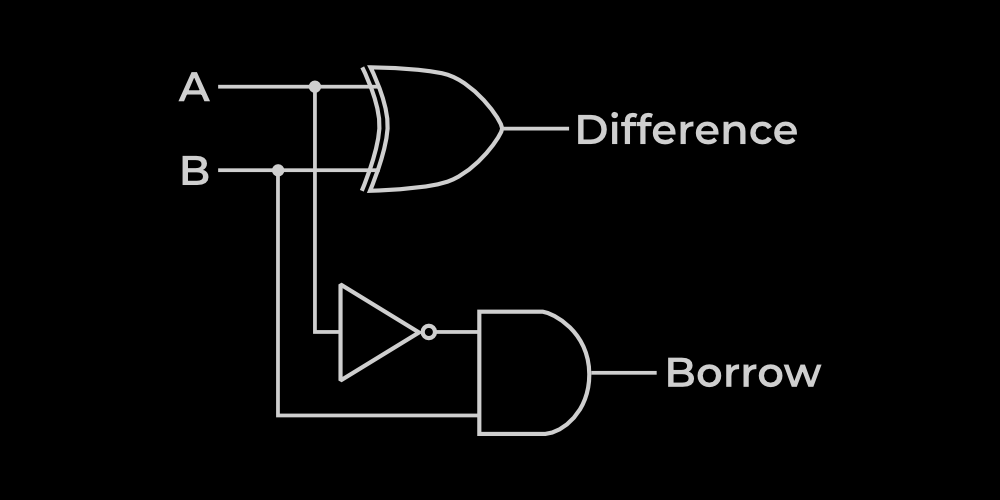
Half Subtractor

Subtract 2, single-digit binary numbers.

A	B	Diff	Borrow
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

!

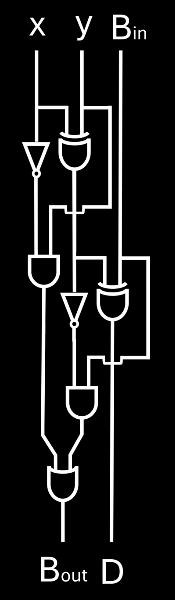
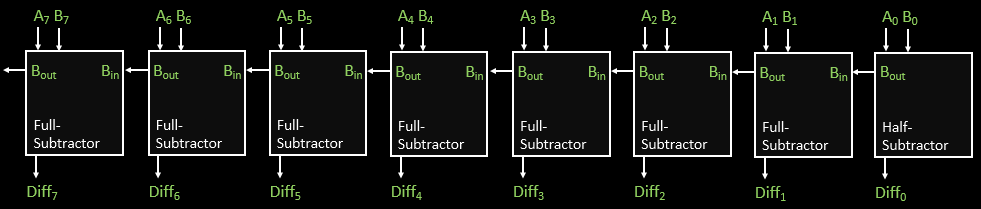
Full Subtractor

A full subtractor accepts the borrow value, allowing us to chain results.

A	B	Bin	Diff	Bout
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

!

8-Bit Subtractor

!

Multiplication

Multiplication is also similar to its decimal counterpart, but because binary is so small compared to decimal, the steps are also much simpler.

First, multiply the top number to every digit of the bottom one, and then add the results together.

X	0	1
0	0	0
1	0	1

    ||.|		
 x  ||.
    ....
   ||.|
+ ||.|
 |..|||.

2-Bit By 2-Bit Multiplier

!

Division

1. Find the smallest part of the dividend greater than or equal to the ==divisor==.

   |.|  ||..|
   

2. Write the first digit of ==the answer==, and ==copy the original divisor down==.

   			 |
   |.|  ||..|
   		 |.|
   

3. Subtract ==the aligned dividend digits== by ==the digits under the dividend==.

   			 |
   |.|  ||..|	 
   		 |.|
   			 |
   

4. Lower ==the next dividend digit==.

   			 |
   |.|  ||..|	 
   		 |.|
   			 |.
   

5. Is ==the total== greater or equal to the ==divisor==? If so, add a 1 to the answer. If not, ==add a== ==0== ==to the answer== ==and return to step 4==.

   			 |.
   |.|  ||..|	 
   		 |.|
   			 |.
   

6. Return to step 2, until you reach the end of the number. If you reached the end, you found ==the answer==.

   			 |.|
   |.|  ||..|	 
   		 |.|
   			 |.|
   			 |.|
   				 .
   

ASCII

Binary can also be used to represent characters.

Dec	Hex	Binary	HTML	Char	Description
0	00	00000000	�	NUL	Null
1	01	00000001		SOH	Start of Heading
2	02	00000010		STX	Start of Text
3	03	00000011		ETX	End of Text
4	04	00000100		EOT	End of Transmission
5	05	00000101		ENQ	Enquiry
6	06	00000110		ACK	Acknowledge
7	07	00000111		BEL	Bell
8	08	00001000		BS	Backspace
9	09	00001001			HT	Horizontal Tab
10	0A	00001010	
	LF	Line Feed
11	0B	00001011		VT	Vertical Tab
12	0C	00001100		FF	Form Feed
13	0D	00001101	
	CR	Carriage Return
14	0E	00001110		SO	Shift Out
15	0F	00001111		SI	Shift In
16	10	00010000		DLE	Data Link Escape
17	11	00010001		DC1	Device Control 1
18	12	00010010		DC2	Device Control 2
19	13	00010011		DC3	Device Control 3
20	14	00010100		DC4	Device Control 4
21	15	00010101		NAK	Negative Acknowledge
22	16	00010110		SYN	Synchronize
23	17	00010111		ETB	End of Transmission Block
24	18	00011000		CAN	Cancel
25	19	00011001		EM	End of Medium
26	1A	00011010		SUB	Substitute
27	1B	00011011		ESC	Escape
28	1C	00011100		FS	File Separator
29	1D	00011101		GS	Group Separator
30	1E	00011110		RS	Record Separator
31	1F	00011111		US	Unit Separator
32	20	00100000	 	space	Space
33	21	00100001	!	!	exclamation mark
34	22	00100010	"	"	double quote
35	23	00100011	#	#	number
36	24	00100100	$	$	dollar
37	25	00100101	%	%	percent
38	26	00100110	&	&	ampersand
39	27	00100111	'	'	single quote
40	28	00101000	(	(	left parenthesis
41	29	00101001	)	)	right parenthesis
42	2A	00101010	*	*	asterisk
43	2B	00101011	+	+	plus
44	2C	00101100	,	,	comma
45	2D	00101101	-	-	minus
46	2E	00101110	.	.	period
47	2F	00101111	/	/	slash
48	30	00110000	0	0	zero
49	31	00110001	1	1	one
50	32	00110010	2	2	two
51	33	00110011	3	3	three
52	34	00110100	4	4	four
53	35	00110101	5	5	five
54	36	00110110	6	6	six
55	37	00110111	7	7	seven
56	38	00111000	8	8	eight
57	39	00111001	9	9	nine
58	3A	00111010	:	:	colon
59	3B	00111011	&#59;	;	semicolon
60	3C	00111100	&#60;	<	less than
61	3D	00111101	&#61;	=	equality sign
62	3E	00111110	&#62;	>	greater than
63	3F	00111111	&#63;	?	question mark
64	40	01000000	&#64;	@	at sign
65	41	01000001	&#65;	A
66	42	01000010	&#66;	B
67	43	01000011	&#67;	C
68	44	01000100	&#68;	D
69	45	01000101	&#69;	E
70	46	01000110	&#70;	F
71	47	01000111	&#71;	G
72	48	01001000	&#72;	H
73	49	01001001	&#73;	I
74	4A	01001010	&#74;	J
75	4B	01001011	&#75;	K
76	4C	01001100	&#76;	L
77	4D	01001101	&#77;	M
78	4E	01001110	&#78;	N
79	4F	01001111	&#79;	O
80	50	01010000	&#80;	P
81	51	01010001	&#81;	Q
82	52	01010010	&#82;	R
83	53	01010011	&#83;	S
84	54	01010100	&#84;	T
85	55	01010101	&#85;	U
86	56	01010110	&#86;	V
87	57	01010111	&#87;	W
88	58	01011000	&#88;	X
89	59	01011001	&#89;	Y
90	5A	01011010	&#90;	Z
91	5B	01011011	&#91;	[	left square bracket
92	5C	01011100	&#92;	|backslash
93	5D	01011101	&#93;	]	right square bracket
94	5E	01011110	&#94;	^	caret / circumflex
95	5F	01011111	&#95;	_	underscore
96	60	01100000	&#96;	`	grave / accent
97	61	01100001	&#97;	a
98	62	01100010	&#98;	b
99	63	01100011	&#99;	c
100	64	01100100	&#100;	d
101	65	01100101	&#101;	e
102	66	01100110	&#102;	f
103	67	01100111	&#103;	g
104	68	01101000	&#104;	h
105	69	01101001	&#105;	i
106	6A	01101010	&#106;	j
107	6B	01101011	&#107;	k
108	6C	01101100	&#108;	l
109	6D	01101101	&#109;	m
110	6E	01101110	&#110;	n
111	6F	01101111	&#111;	o
112	70	01110000	&#112	p
113	71	01110001	&#113;	q
114	72	01110010	&#114;	r
115	73	01110011	&#115;	s
116	74	01110100	&#116;	t
117	75	01110101	&#117;	u
118	76	01110110	&#118;	v
119	77	01110111	&#119;	w
120	78	01111000	&#120;	x
121	79	01111001	&#121;	y
122	7A	01111010	&#122;	z
123	7B	01111011	&#123;	{	left curly bracket
124	7C	01111100	&#124;	|	vertical bar
125	7D	01111101	&#125;	}	right curly bracket
126	7E	01111110	&#126;	~	tilde
127	7F	01111111	&#127;	DEL	delete