web/content/notes/ready/how_to_computer/index.md

title, description, draft, tags, author, showToc, weight

title	description	draft	tags	author	showToc	weight
Building a Computer From Scratch		false	electronics computer-science	TrudeEH	true	1

Diodes

A diode allows current to only flow in one direction in a circuit.

Schematic

Anode (+) --|>|-- Cathode (-)

Examples

[Conventional Current (+) -> (-)]
(+)------|>|------(-)   Current can flow - The diode is now a conductor.
(+)------|<|------(-)   Current can't flow - The diode is now an insulator.

Use Cases

• Protect a circuit (if a battery is connected incorrectly, for example)
• Convert AC to DC current
  Fun fact: An LED, for example, is a Light-Emitting Diode.

How a Diode Works

Conductors and Insulators

An atom contains the following elements:

• Nucleus (Protons - Neutrons)
• Orbital Shells (Holds the electrons, which orbit around the nucleus)
• Conduction band
  The electrons closest to the nucleus hold the most energy.
  The outermost shell is the valence shell. A conductor has 1-3 electrons in the valence shell.
  If an electron reaches the conduction band, it can break free and move to another atom.
  An insulator, however, has a conduction band that is far from the valence shell, making it difficult for an electron to escape.
  For example, for copper (a great conductor), the valence shell and conduction band overlap, so it's very easy for an electron to jump between atoms.
  Semiconductors have a conduction band close to the valence shell, but have one extra electron in it, making it an insulator. However, given some external energy, some electrons will gain enough energy to reach the conduction band and become free.

P-Type and N-Type Doping

Silicon is a good semiconductor, having 4 electrons in its valence shell. When close to other Si atoms, they share 4 electrons with their neighbors, thus, having 8, each, and becoming stable.

Silicon:
Si Si Si Si Si Si Si Si Si Si Si
Si Si Si Si Si Si Si Si Si Si Si
Si Si Si Si Si Si Si Si Si Si Si
Si Si Si Si Si Si Si Si Si Si Si
Si Si Si Si Si Si Si Si Si Si Si
Si Si Si Si Si Si Si Si Si Si Si

N-Type

Some Phosphorus is added to the Silicon. ==p== has one extra electron in its valence shell.
These electrons are not needed, and so, they flow freely from atom to atom.

Si Si p Si Si Si Si Si Si Si p
p Si Si Si Si p Si Si Si Si Si
Si Si Si p Si Si Si Si p Si Si
Si p Si Si p Si Si Si Si Si Si
Si Si Si Si Si Si p Si Si p Si
Si p Si Si Si Si Si Si p Si Si

P-Type

Some Aluminum is added to the Silicon. Al is missing one electron, so it can't provide its 4 neighbors with an electron to share.

Si Si Al Si Si Si Si Si Si Si Al
Al Si Si Si Si Al Si Si Si Si Si
Si Si Si Al Si Si Si Si Al Si Si
Si Al Si Si Al Si Si Si Si Si Si
Si Si Si Si Si Si Al Si Si Al Si
Si Al Si Si Si Si Si Si Al Si Si

Combining both Types

When an N-Type is combined with a P-Type, some electrons from the N-Type side will move over to the P-Type side and occupy the missing electrons there. This creates a barrier between both types, creating an electric field that prevents more electrons from switching sides.

Forward Bias

If energy is provided to the Cathode, the electrons flow, as the voltage is superior to the barrier's.

(-)-----[P|N]-----(+)

Reverse Bias

If energy is provided to the Anode, the electrons can't flow, as the barrier expands.

(-)--[P]      [N]--(+)

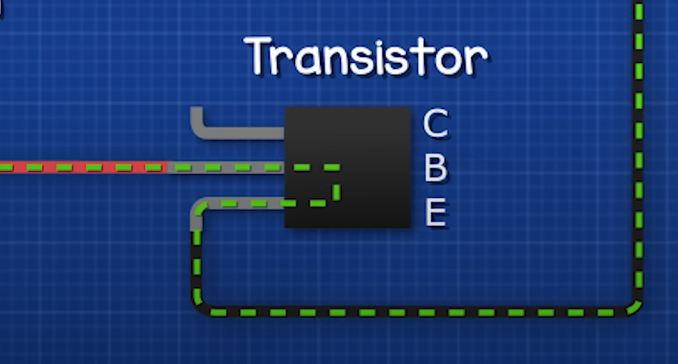
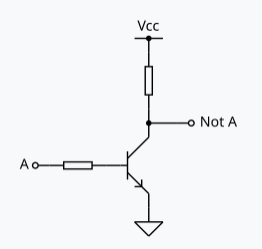
Transistor

Transistors are electronic components that behave like a switch, or amplifier.

Schematic

        .--.,-- Collector
Base --(--|<)
        `--`'-- Emitter

Examples

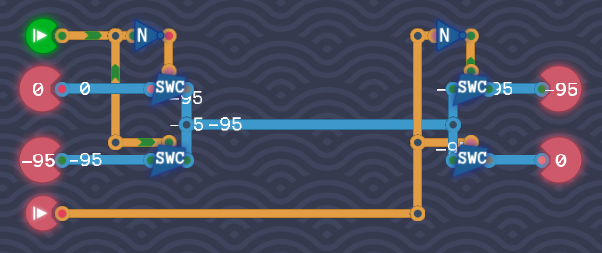
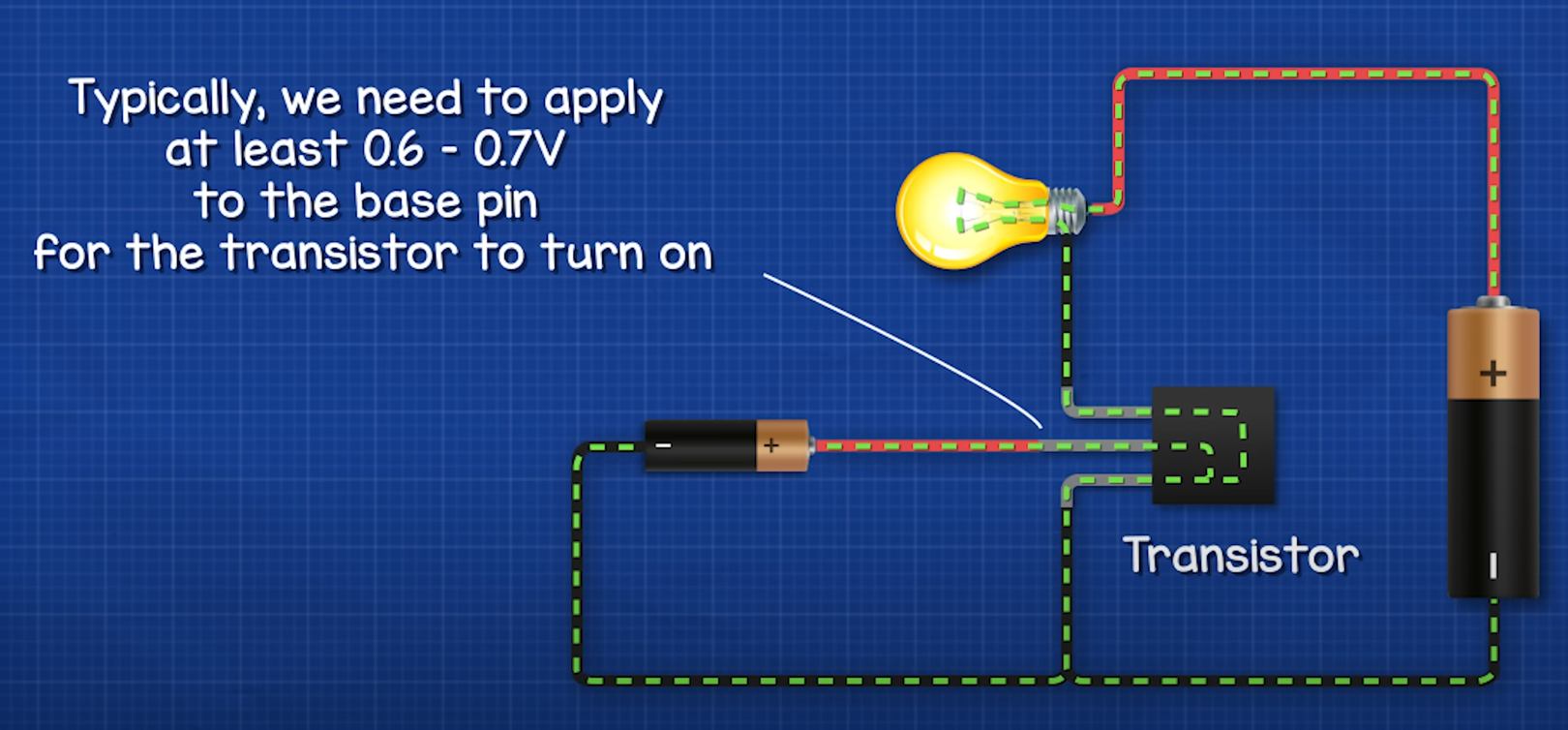
Switch

If the base pin is provided with energy, the transistor allows current to flow in the main circuit.
!

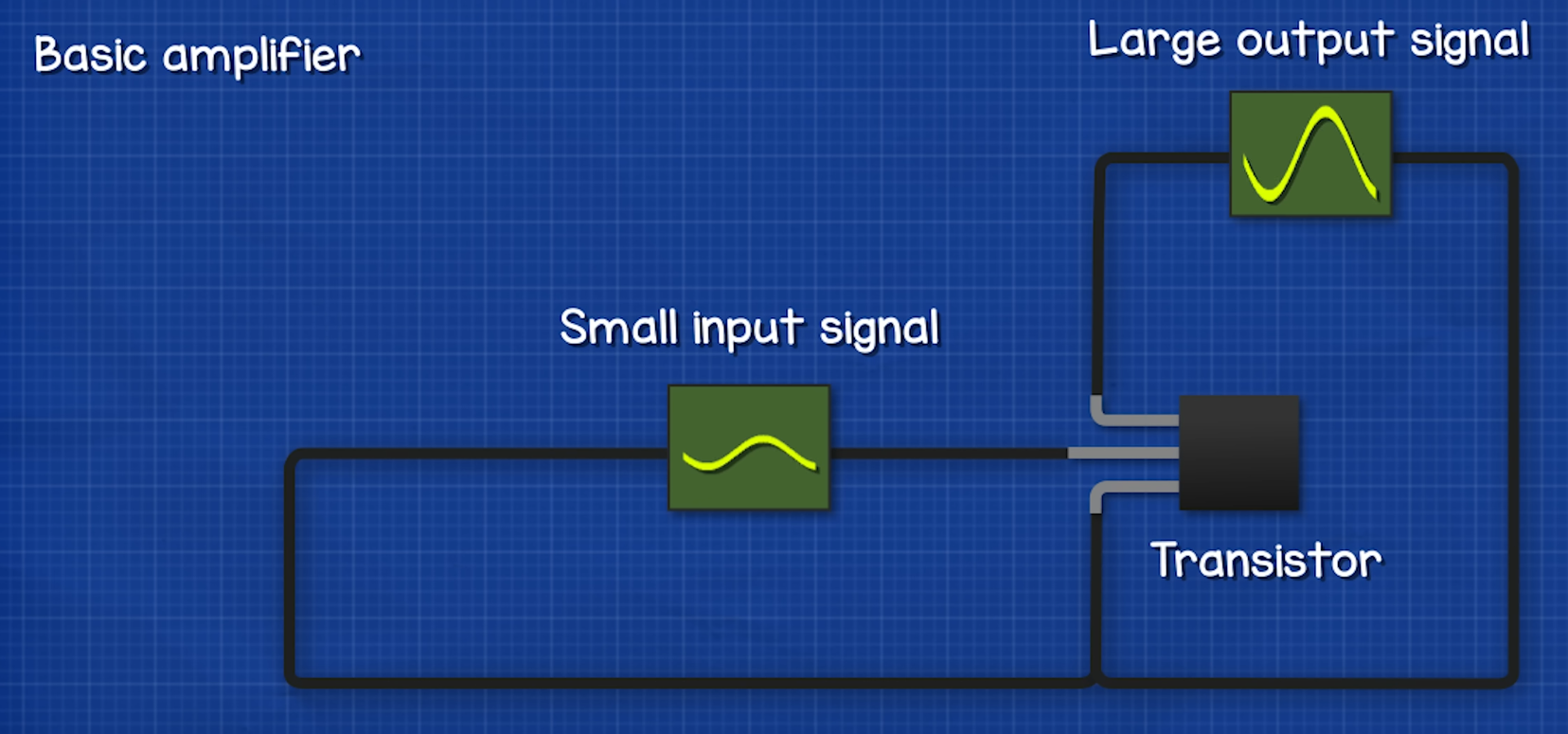
Amplifier

Altering the voltage given to the base pin allows us to control a larger voltage in the main circuit.

Types of Transistor

NPN

An NPN transistor combines the base pin and collector pin.

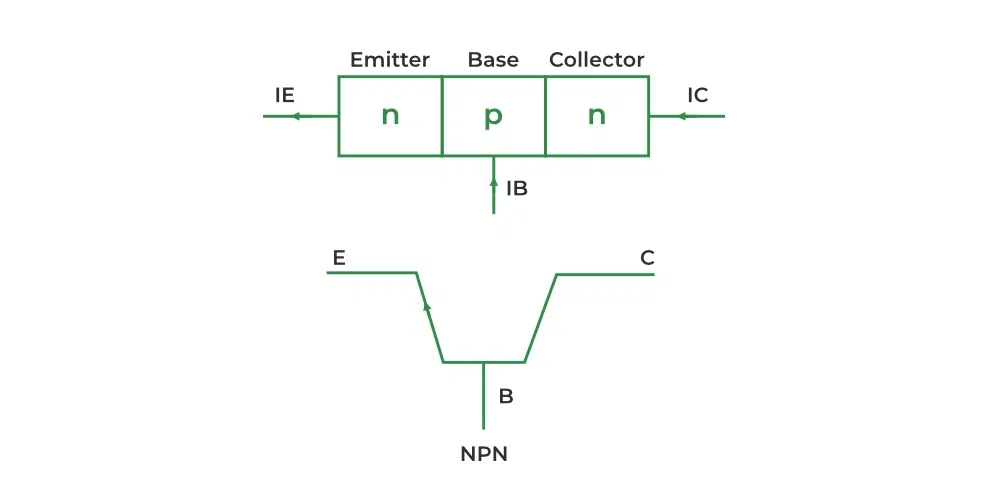
Note: Even if the collector pin is disconnected from the circuit, a small amount of current still passes through.

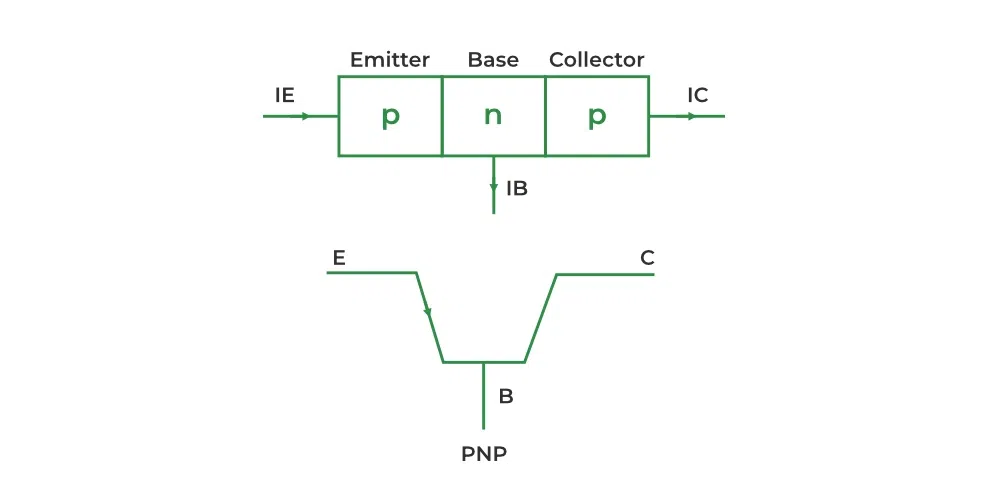
PNP

A PNP transistor receives energy through the emitter pin, and then divides it to the remaining pins.

Basic Logic

A logic gate is a device that performs one boolean operation: Two binary inputs produce a single binary output. These building blocks are the foundations of modern computing.
Each gate has its own truth table, which defines every possible input and output variations.

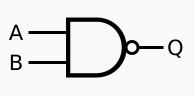
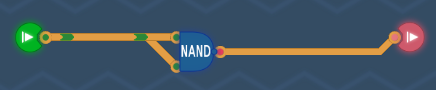
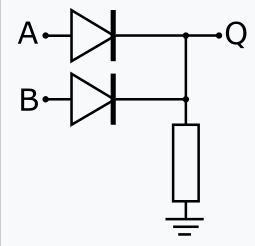
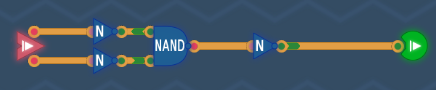
NAND

A NAND gate can be used to build all other basic gates. It always outputs, unless both inputs are active.

Truth Table

A	B	Output
0	0	1
0	1	1
1	0	1
1	1	0

Implementation

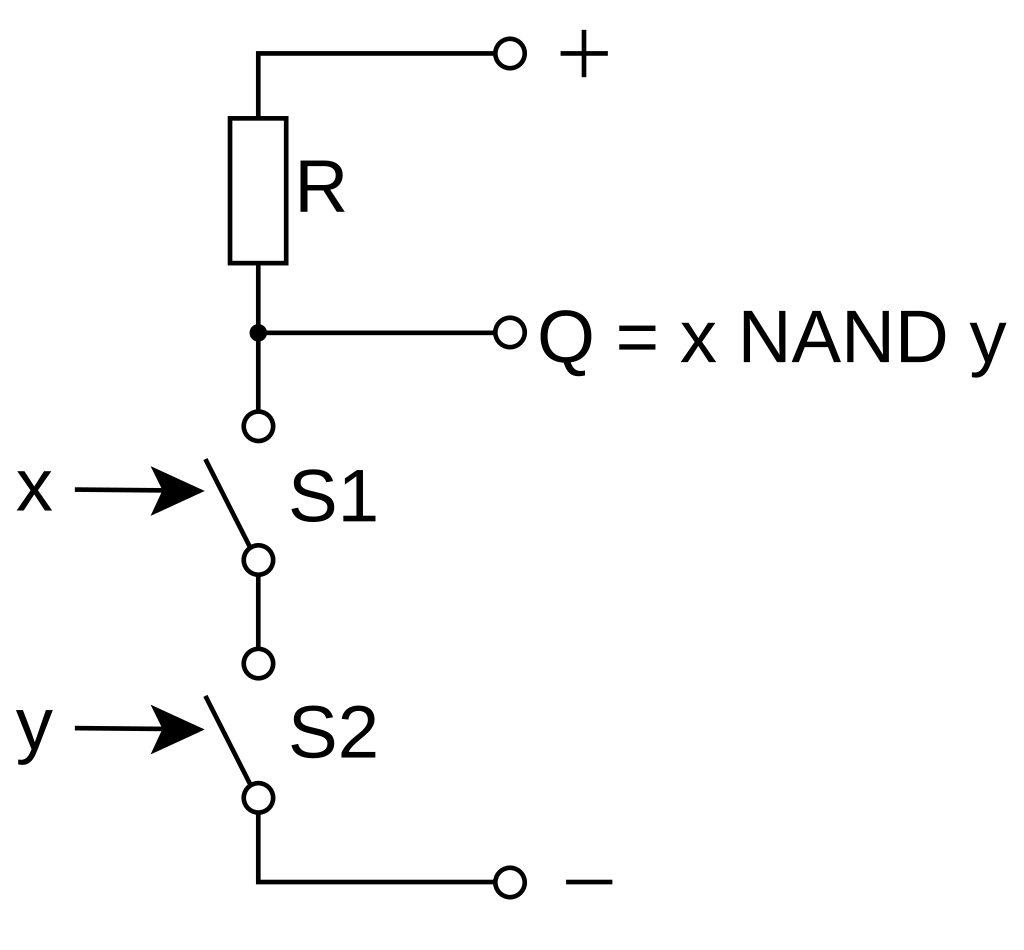
Electronics

Implementation using switches (transistors could be used instead) and a pull-up resistor:
!

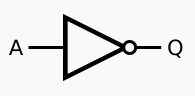
NOT

Invert any given input.

Truth Table

Input	Output
0	1
1	0

Implementation

Logic Gates

!

Electronics

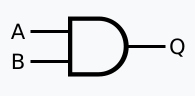
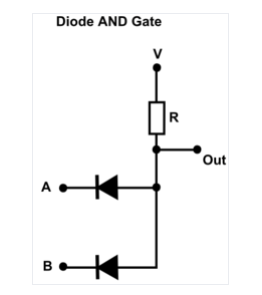
AND

Outputs 1 only when both inputs are 1.

Truth Table

A	B	Output
0	0	0
0	1	0
1	0	0
1	1	1

Implementation

Logic Gates

!

Electronics

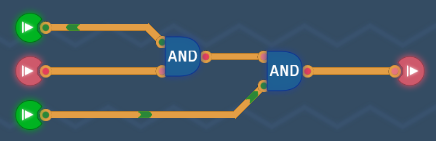
Bigger AND Gate

AND gates can be chained to accept more inputs.

!

Truth Table

A	B	C	Output
0	0	0	0
0	1	0	0
1	0	0	0
1	1	0	0
0	0	1	0
0	1	1	0
1	0	1	0
1	1	1	1

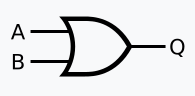
OR

Outputs 1 if at least one input is 1.

Truth Table

A	B	Output
0	0	0
0	1	1
1	0	1
1	1	1

Implementation

Logic Gates

!

Electronics

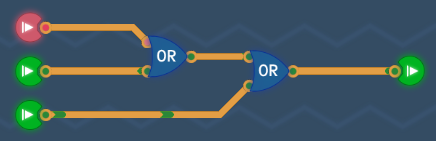
Bigger OR Gate

!

Truth Table

A	B	C	Output
0	0	0	0
0	1	0	1
1	0	0	1
1	1	0	1
0	0	1	1
0	1	1	1
1	0	1	1
1	1	1	1

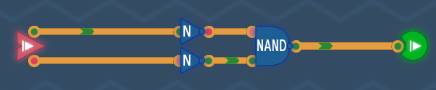
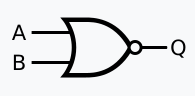
NOR

An OR gate followed by a NOT gate.

A NOR gate is can also be used to build every other gate, just like NAND. However, NAND gates are preferred over NOR gates, as, in modern computers, they occupy less area and have less delay.

Truth Table

A	B	Output
0	0	1
0	1	0
1	0	0
1	1	0

Implementation

Logic Gates

!

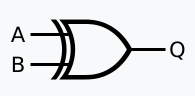
XOR

Either input is 1, exclusively. (OR, but if both inputs are on, it turns off.)

Truth Table

A	B	Output
0	0	0
0	1	1
1	0	1
1	1	0

Implementation

Logic Gates

!

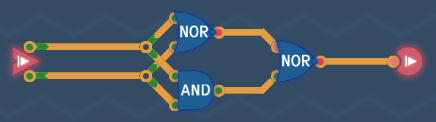
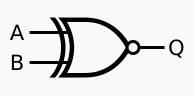
XNOR

Inverted XOR.

Truth Table

A	B	Output
0	0	1
0	1	0
1	0	0
1	1	1

Implementation

Logic Gates

!

Although this circuits works, it can be further optimized to save 1 gate.

!

From this point on, circuits will become exponentially more complex. Optimizations like this one can be found almost everywhere, however, when the choice between efficiency and readability arises, I will choose to keep things simple. If you found a way to optimize any of my circuits, please let me know. I'd be happy to keep improving these notes, and credit you for your findings.

Binary

Binary is a base-2 numeral system: A simple way to represent numbers using only two states. Each binary 'digit' is called a bit, and 8 bits together form a byte.
To represent large binary values, it's common to use hexadecimal as well, to shorten them into a more readable format.

Binary	Decimal	Hexadecimal
0000	00	0
0001	01	1
0010	02	2
0011	03	3
0100	04	4
0101	05	5
0110	06	6
0111	07	7
1000	08	8
1001	09	9
1010	10	A
1011	11	B
1100	12	C
1101	13	D
1110	14	E
1111	15	F

Arithmetic Operations

Addition

Adding two numbers can be done using a simple, manual algorithm: By adding the last bit of both numbers first, carry if necessary, then move to the next number, and so on.

+	0	1
0	0	1
1	1	10

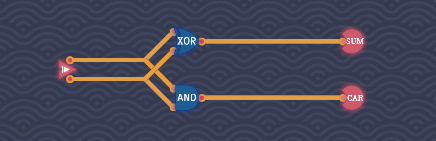
Half Adder

Add 2, single-digit binary numbers.

A	B	Carry	Sum
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

!

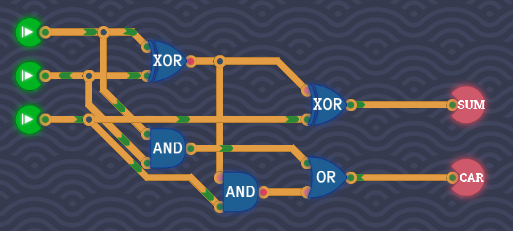
Full Adder (ADD)

When adding 2 binary numbers, one operation might return a carry value, which the half adder can't accept, as it only has 2 inputs.

To solve this issue, a full adder accepts 3 inputs.

!

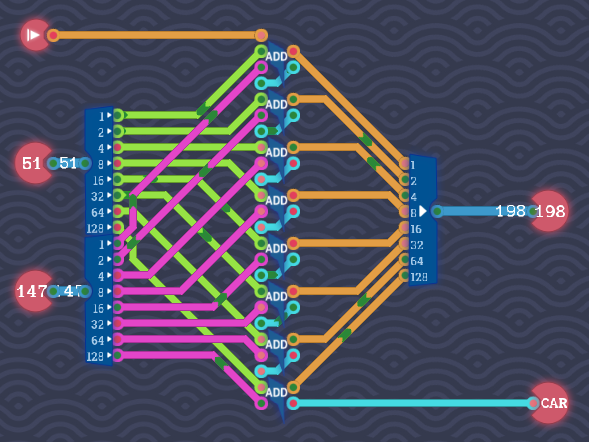
8-Bit Adder

To add two bytes, chain 8 full-adders.
(The dark blue lines are equivalent to 8 bits in parallel, simplified for better readability. The blue rectangles split the wire into 8 bits, or vice versa.)

!

Two's Complement

The most common solution to represent negative numbers is to interpret the last bit as a negative value. For a byte, the last bit changes its value from 128 to -128.

A negative number is often called a signed number.

The main advantage of the Two's Complement system is that the adder built previously also works with it.

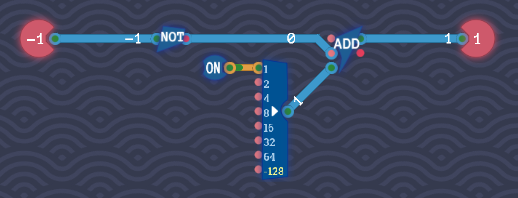
Invert Sign

To switch between negative and positive numbers, flip all bits, then add 1.

!

Subtraction

Subtraction is as easy as negating (inverting the sign of) the second input.

!

Multiplication

Multiplication is also similar to its decimal counterpart, but because binary is so small compared to decimal, the steps are also much simpler.

First, multiply the top number to every digit of the bottom one, and then add the results together.

X	0	1
0	0	0
1	0	1

2-Bit By 2-Bit Multiplier

4-Bit By 4-Bit Multiplier

!

Division

Division is more complex. So much so, that it is often implemented in code, instead of hardware. For example, ARM CPUs don't have an instruction for division.
Harder doesn't mean impossible of course, and if you are curious, there are many resources you can see. For example: This Reddit post; YouTube Video.

The steps for binary division are as follows:

1. Find the smallest part of the dividend greater than or equal to the divisor.

2. Write the first digit of the answer, and copy the original divisor down.

3. Subtract the aligned dividend digits by the digits under the dividend.

4. Lower the next dividend digit.
   

5. Is the total greater or equal to the divisor? If so, add a 1 to the answer. If not, add a 0 to the answer and return to step 4.
   

6. Return to step 2, until you reach the end of the number. If you reached the end, you found the answer.
   

Memory

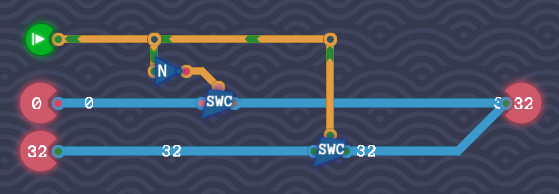
Byte Switch (SWC)

A bit switch, also known as a transistor, toggles a given input, using a second bit.

!

If 8 transistors are controlled by the same bit in parallel, a Byte Switch is created.

Input Selector

Using byte switches, we can select which input to use.

!

Bus

A Bus is useful to simplify wiring. One bit controls which input should be selected, and a second one, the output. This way, a single wire can transfer twice as much information.

!

1 Bit of Memory

There are many ways to achieve a bit of memory.

Using Transistors and a Tick Delay

The oval component is a delay. This replaces the concept of a clock, however, in an electronic circuit, the save and load states are attached to a clock instead.

!

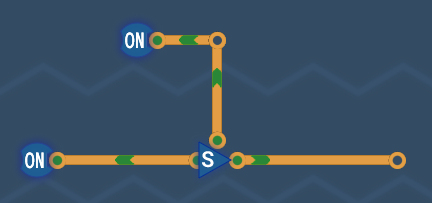
SR Latch

A Set-Reset Latch is the simplest one. The S input sets the output to 1, and the R input, to 0. If both inputs are on, the latch is in an undefined state, and outputs 0.

!

D Latch

8bit Register

After obtaining one bit of memory, a byte of memory can be built.

!

Binary Decoder

A decoder splits two states of a bit into two separate outputs.

!

3bit Decoder

!

---

Registers

A single bit isn't very useful, so we can use the previous circuit to create an 8bit register.

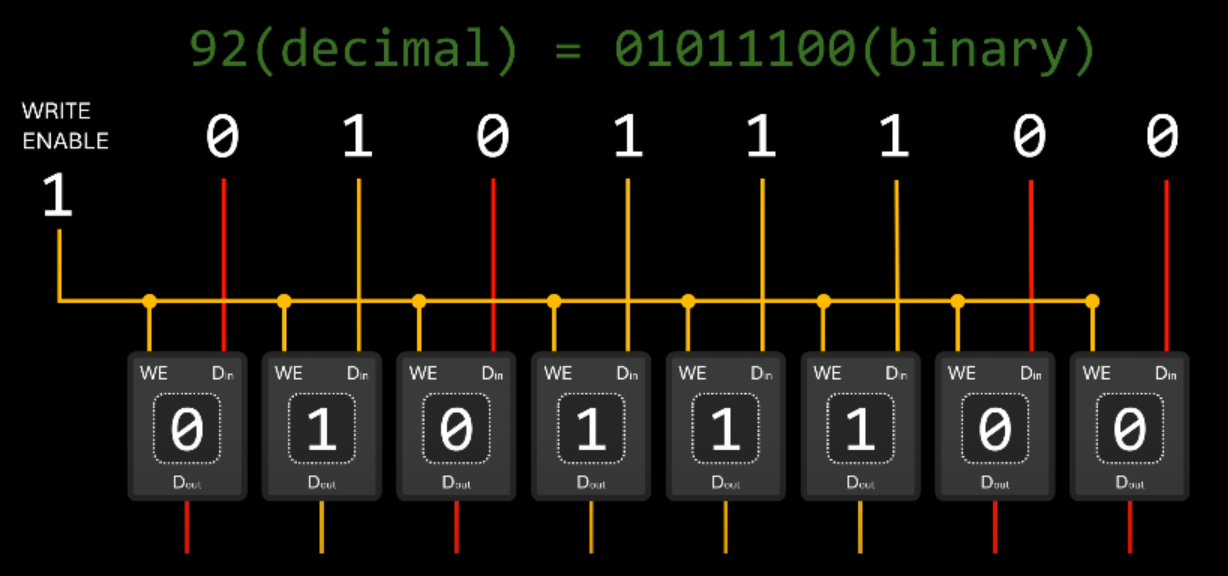
Binary Decoder

Select which circuit to activate, depending on the task at hand.

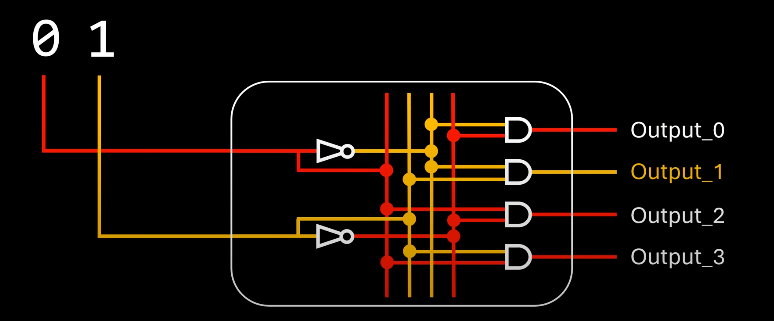
RAM

Registers don't scale well, however, as storing a large amount of data would require millions of wires.
We can organize latches in a matrix instead of a long, horizontal line.

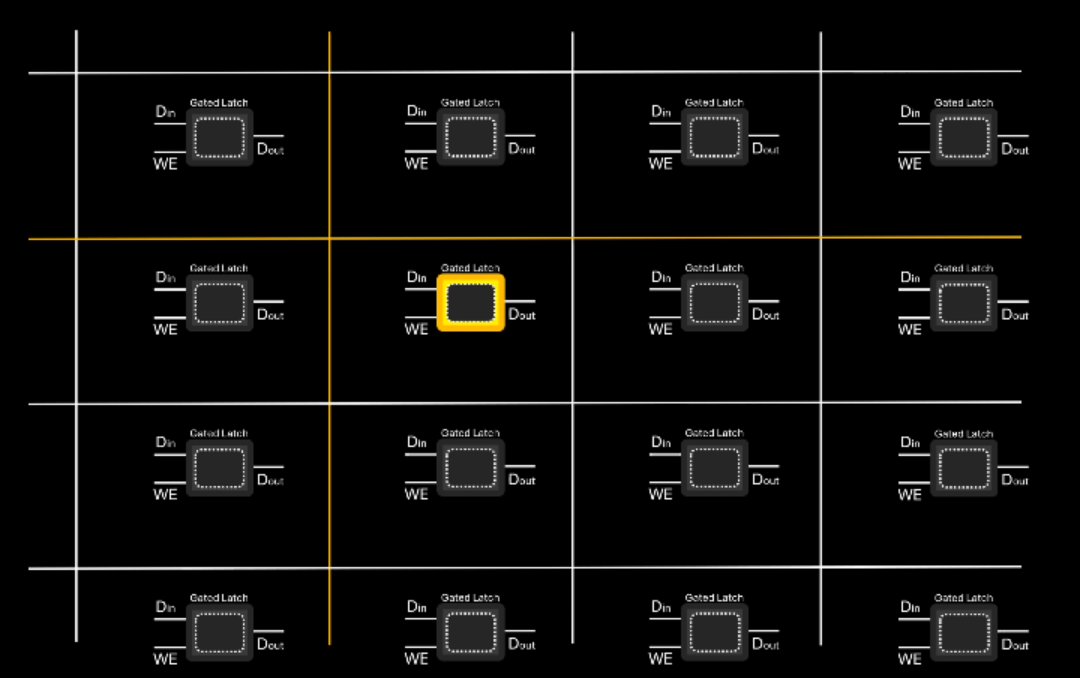
To access a specific latch, binary decoders can be used.

This way, a single, short memory address can select any latch in the matrix.

Reading and Writing to the Matrix

We can modify the latch to reduce the amount of wires needed.

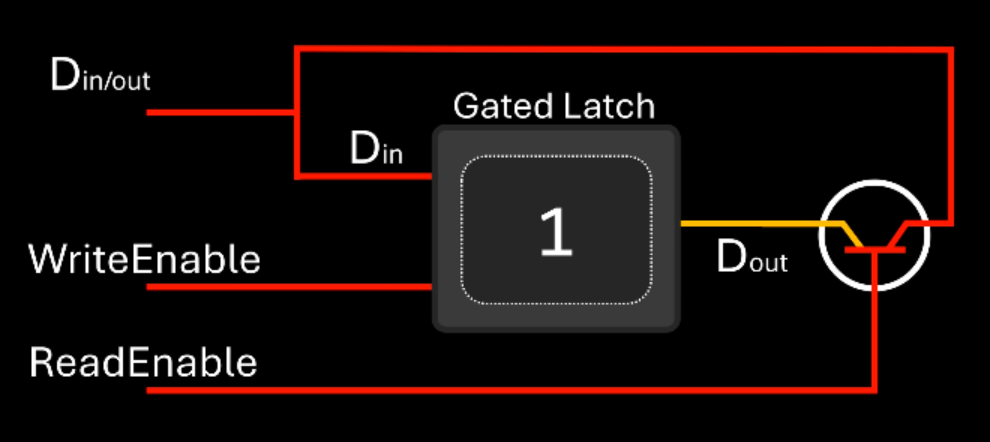
This new latch uses the same wire for both input and output.

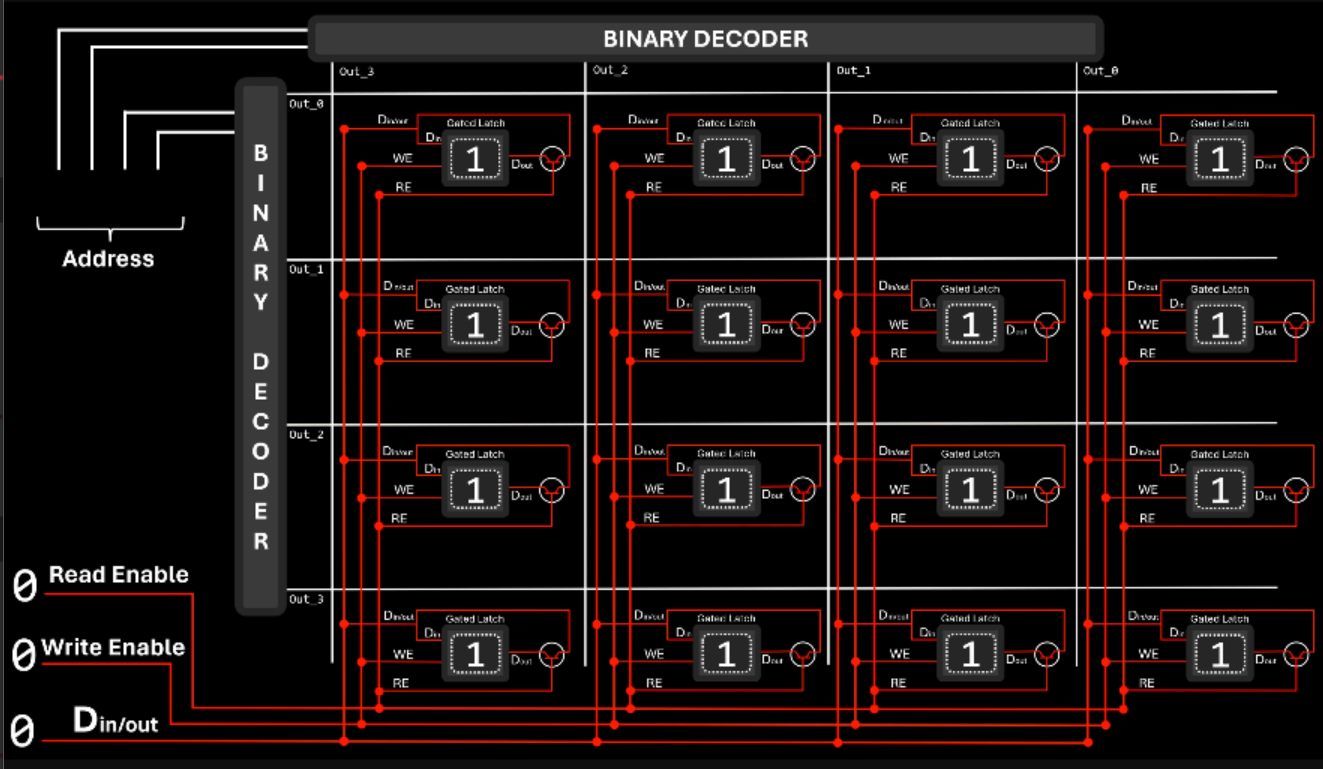
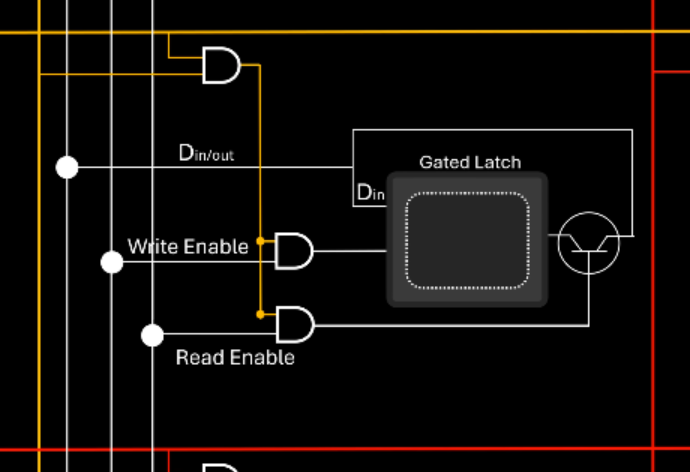
This circuit would store the same value on every latch, which isn't useful. With some modifications, however, we can use the memory address to select which latch to modify.

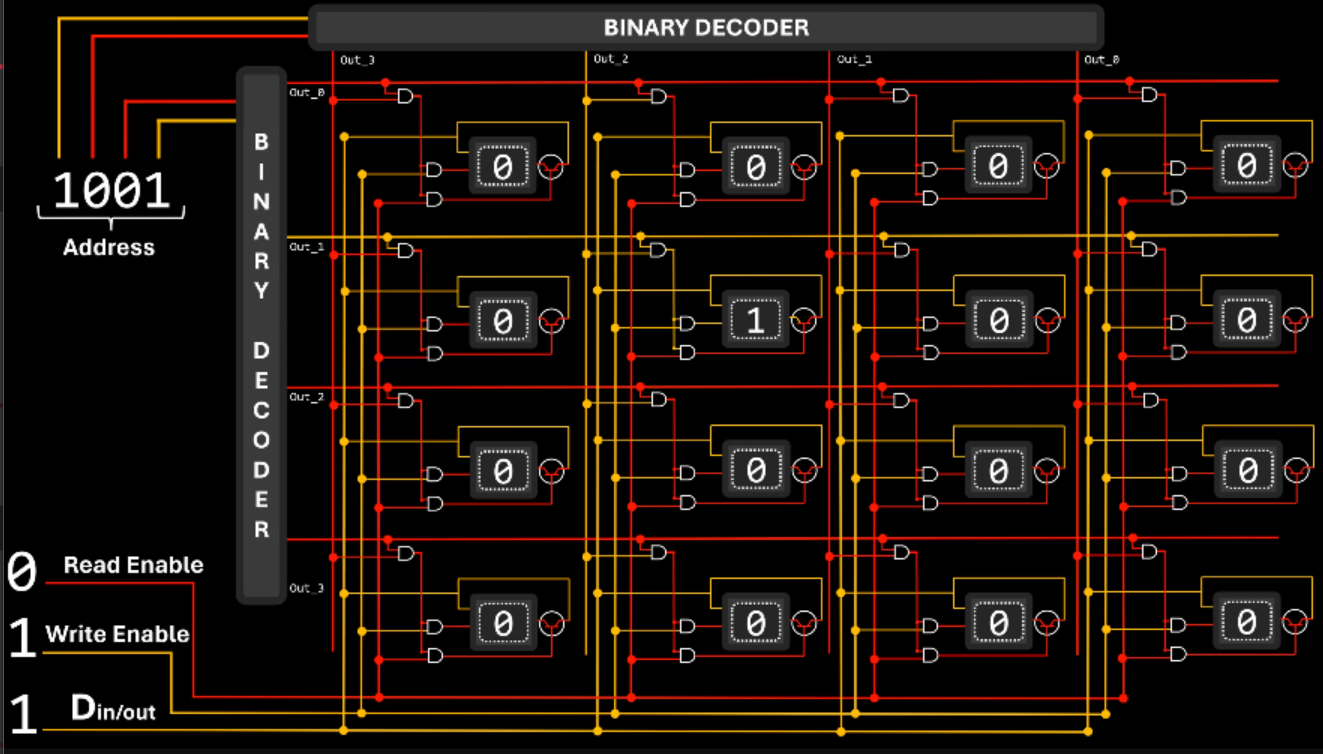
Storing Bytes Instead of Bits

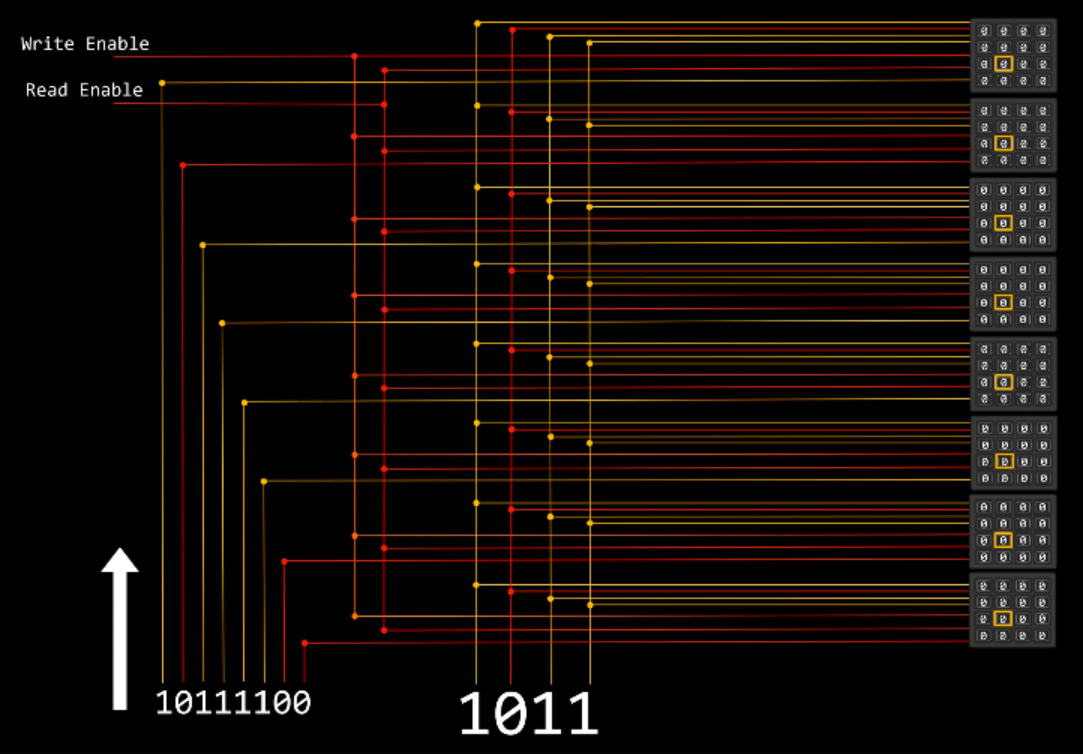
In this example, we can provide 1 byte of information, a write or read signal, and a memory address. Since we are storing a full byte, the same memory address applies for all 8, single bit circuits.
This configuration is more commonly known as RAM.
To make it easier to understand, we can abstract these concepts further.

The largest the Address Bus is, the more bits can be managed. This is why a 32bit CPU can't manage more than 4 GB of RAM.

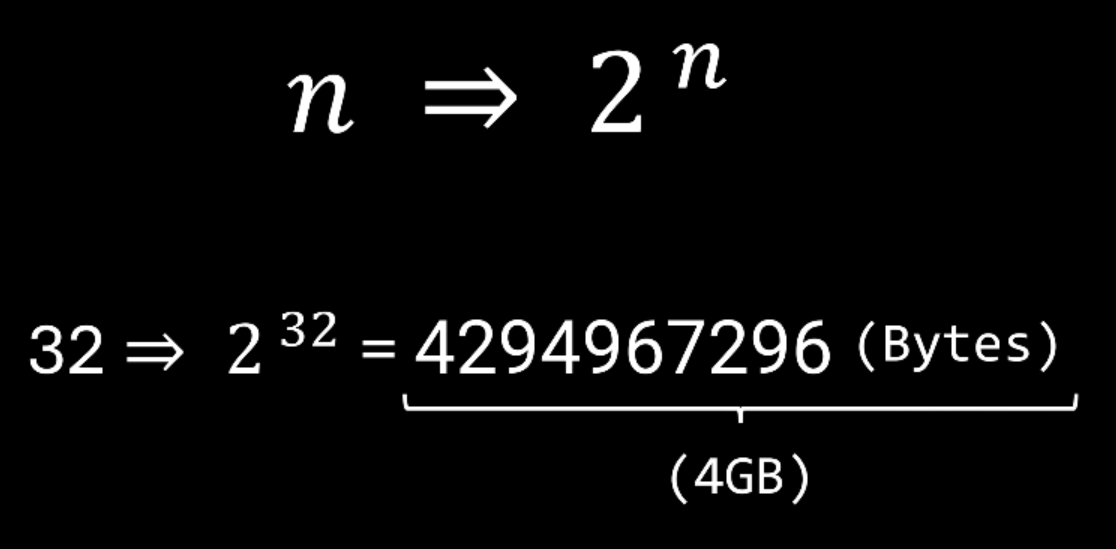
This kind of RAM is Static RAM (SRAM), which uses many transistors, making it faster, but more expensive to produce than DRAM.

ASCII

Binary can also be used to represent characters.

Dec	Hex	Binary	HTML	Char	Description
0	00	00000000	�	NUL	Null
1	01	00000001		SOH	Start of Heading
2	02	00000010		STX	Start of Text
3	03	00000011		ETX	End of Text
4	04	00000100		EOT	End of Transmission
5	05	00000101		ENQ	Enquiry
6	06	00000110		ACK	Acknowledge
7	07	00000111		BEL	Bell
8	08	00001000		BS	Backspace
9	09	00001001			HT	Horizontal Tab
10	0A	00001010	
	LF	Line Feed
11	0B	00001011		VT	Vertical Tab
12	0C	00001100		FF	Form Feed
13	0D	00001101	
	CR	Carriage Return
14	0E	00001110		SO	Shift Out
15	0F	00001111		SI	Shift In
16	10	00010000		DLE	Data Link Escape
17	11	00010001		DC1	Device Control 1
18	12	00010010		DC2	Device Control 2
19	13	00010011		DC3	Device Control 3
20	14	00010100		DC4	Device Control 4
21	15	00010101		NAK	Negative Acknowledge
22	16	00010110		SYN	Synchronize
23	17	00010111		ETB	End of Transmission Block
24	18	00011000		CAN	Cancel
25	19	00011001		EM	End of Medium
26	1A	00011010		SUB	Substitute
27	1B	00011011		ESC	Escape
28	1C	00011100		FS	File Separator
29	1D	00011101		GS	Group Separator
30	1E	00011110		RS	Record Separator
31	1F	00011111		US	Unit Separator
32	20	00100000	 	space	Space
33	21	00100001	!	!	exclamation mark
34	22	00100010	"	"	double quote
35	23	00100011	#	#	number
36	24	00100100	$	$	dollar
37	25	00100101	%	%	percent
38	26	00100110	&	&	ampersand
39	27	00100111	'	'	single quote
40	28	00101000	(	(	left parenthesis
41	29	00101001	)	)	right parenthesis
42	2A	00101010	*	*	asterisk
43	2B	00101011	+	+	plus
44	2C	00101100	,	,	comma
45	2D	00101101	-	-	minus
46	2E	00101110	.	.	period
47	2F	00101111	/	/	slash
48	30	00110000	0	0	zero
49	31	00110001	1	1	one
50	32	00110010	2	2	two
51	33	00110011	3	3	three
52	34	00110100	4	4	four
53	35	00110101	5	5	five
54	36	00110110	6	6	six
55	37	00110111	7	7	seven
56	38	00111000	8	8	eight
57	39	00111001	9	9	nine
58	3A	00111010	:	:	colon
59	3B	00111011	&#59;	;	semicolon
60	3C	00111100	&#60;	<	less than
61	3D	00111101	&#61;	=	equality sign
62	3E	00111110	&#62;	>	greater than
63	3F	00111111	&#63;	?	question mark
64	40	01000000	&#64;	@	at sign
65	41	01000001	&#65;	A
66	42	01000010	&#66;	B
67	43	01000011	&#67;	C
68	44	01000100	&#68;	D
69	45	01000101	&#69;	E
70	46	01000110	&#70;	F
71	47	01000111	&#71;	G
72	48	01001000	&#72;	H
73	49	01001001	&#73;	I
74	4A	01001010	&#74;	J
75	4B	01001011	&#75;	K
76	4C	01001100	&#76;	L
77	4D	01001101	&#77;	M
78	4E	01001110	&#78;	N
79	4F	01001111	&#79;	O
80	50	01010000	&#80;	P
81	51	01010001	&#81;	Q
82	52	01010010	&#82;	R
83	53	01010011	&#83;	S
84	54	01010100	&#84;	T
85	55	01010101	&#85;	U
86	56	01010110	&#86;	V
87	57	01010111	&#87;	W
88	58	01011000	&#88;	X
89	59	01011001	&#89;	Y
90	5A	01011010	&#90;	Z
91	5B	01011011	&#91;	[	left square bracket
92	5C	01011100	&#92;	|backslash
93	5D	01011101	&#93;	]	right square bracket
94	5E	01011110	&#94;	^	caret / circumflex
95	5F	01011111	&#95;	_	underscore
96	60	01100000	&#96;	`	grave / accent
97	61	01100001	&#97;	a
98	62	01100010	&#98;	b
99	63	01100011	&#99;	c
100	64	01100100	&#100;	d
101	65	01100101	&#101;	e
102	66	01100110	&#102;	f
103	67	01100111	&#103;	g
104	68	01101000	&#104;	h
105	69	01101001	&#105;	i
106	6A	01101010	&#106;	j
107	6B	01101011	&#107;	k
108	6C	01101100	&#108;	l
109	6D	01101101	&#109;	m
110	6E	01101110	&#110;	n
111	6F	01101111	&#111;	o
112	70	01110000	&#112	p
113	71	01110001	&#113;	q
114	72	01110010	&#114;	r
115	73	01110011	&#115;	s
116	74	01110100	&#116;	t
117	75	01110101	&#117;	u
118	76	01110110	&#118;	v
119	77	01110111	&#119;	w
120	78	01111000	&#120;	x
121	79	01111001	&#121;	y
122	7A	01111010	&#122;	z
123	7B	01111011	&#123;	{	left curly bracket
124	7C	01111100	&#124;	|	vertical bar
125	7D	01111101	&#125;	}	right curly bracket
126	7E	01111110	&#126;	~	tilde
127	7F	01111111	&#127;	DEL	delete